2016年2月14日 星期日

2016.2.14 - bayesian, Principle of maximum entropy


Principle of maximum entropy
-熵定义的实际上是一个随机变量的不确定性，熵最大的时候，说明随机变量最不确定，换句话说，也就是随机变量最随机，对其行为做准确预测最困难。

-熵原理本质上仅是“高概率的事物容易出现”


Why maximum entropy

例如，我们只知道一个班的学生考试成绩有三个分数档：80分、90分、100分，且已知平均成绩为90分。显然在这种情况下，三种分数档的概率分布并不是唯一的。因为在下列已知条件限制下
（平均成绩）
（概率归一化条件）
有无限多组解，该选哪一组解呢？即如何从这些相容的分布中挑选出“最佳的”、“最合理”的分布来呢？这个挑选标准就是最大信息熵原理。


Neville's algorithm

p_{0,0}(x) = y_0 \,
p_{0,1}(x) \,
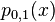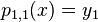p_{1,1}(x) = y_1 \, p_{0,2}(x) \,
p_{1,2}(x) \, p_{0,3}(x) \,
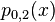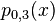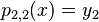p_{2,2}(x) = y_2 \, p_{1,3}(x) \, p_{0,4}(x) \,
p_{2,3}(x) \, p_{1,4}(x) \,
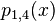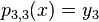p_{3,3}(x) = y_3 \, p_{2,4}(x) \,
p_{3,4}(x) \,
p_{4,4}(x) = y_4 \,




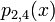Lagrange multiplier

a good tool to find maximum entropy 
is a strategy for finding the local maxima and minima of a function subject to equality constraints.
For instance (see Figure 1), consider the optimization problem
maximize f(x, y)
subject to g(x, y) = 0.
We need both f and g to have continuous first partial derivatives. We introduce a new variable (λ) called a Lagrange multiplier and study the Lagrange function (or Lagrangian) defined by
\mathcal{L}(x,y,\lambda) = f(x,y) - \lambda \cdot g(x,y),


  • Probability axioms

    These assumptions can be summarised as follows: Let (Ω, F, P) be a measure space with P(Ω)=1. Then (Ω, F, P) is a probability space, with sample space Ω, event space F and probability measure P.

    第一公理[編輯]

    對於任意一個集合E\in \mathfrak{F}， 即對於任意的事件P(E)\in [0,1]。
    即，任一事件的機率都可以用0到1區間上的一個實數來表示。

    第二公理[編輯]

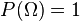    P(\Omega) = 1。
    即，整體樣本集合中的某個基本事件發生的機率為1。更加明確地說，在樣本集合之外已經不存在基本事件了。
    這在一些錯誤的機率計算中經常被小看；如果你不能準確地定義整個樣本集合，那麼任意子集的機率也不可能被定義。

    第三公理[編輯]

    任意兩兩不相交事件E_1, E_2, ...的可數序列滿足P(E_1 \cup E_2 \cup \cdots) = \sum P(E_i)。
    即，不相交子集的並的事件集合的機率為那些子集的機率的和。這也被稱為是σ可加性。如果存在子集間的重疊，這一關係不成立。
    如想通過代數了解柯爾莫果洛夫的方法，請參照隨機變量代數。

    從柯爾莫果洛夫公理可以推導出另外一些對計算機率有用的法則。
    P(A \cup B) = P(A) + P(B) - P(A \cap B)，
    P(\Omega - E) = 1 - P(E)，
    P(A \cap B) = P(A) \cdot P(B \vert A)，
    這一關係給出了貝葉斯定理。以此可以得出A和B是獨立的若且唯若
    P(A \cap B) = P(A) \cdot P(B)，


     Explain why

    假如我錯過了看世界盃，賽後我問一個知道比賽結果的觀眾“哪支球隊是冠軍”？ 他不願意直接告訴我， 而要讓我猜，並且我每猜一次，他就要收一元錢才肯告訴我是否猜對了，那麼我需要付給他多少錢才能知道誰是冠軍呢? 
    我可以把球隊編上號，從 1 到 32， 然後提問： “冠軍的球隊在 1-16 號中嗎?” 假如他告訴我猜對了， 我會接著問： “冠軍在 1-8 號中嗎?” 假如他告訴我猜錯了， 我自然知道冠軍隊在 9-16 中。 這樣只需要猜五次， 我就能知道哪支球隊是冠軍。所以，誰是世界盃冠軍這條消息的信息量只值五塊錢。
    當然，香農不是用錢，而是用 bit的個概念來度量信息量。 一個bit是一位元二進位數字，電腦的一個位元組(byte)是八個bit。
    上面的例子中，這條消息的信息量是五 bit。如果有六十四個隊進入決賽，那麼“誰世界盃冠軍”的信息量就會是6個 bit。到此我們可以發現：原來    香農的信息量( bit數)來自：所有可能結果的 log 函數；log32=5, log64=6。 

    張貼者： 於

    沒有留言:

    張貼留言

    訂閱： 張貼留言 (Atom)